■ 신경망을 학습시키는 여러 기술들 소개(경사하강법의 종류, 배치 정규화, 드롭아웃)
1. 고급 경사 감소법들----------->underfitting 을 막기 위해
2. 가중치 초기화값 설정--------->underfitting 을 막기 위해
3. 배치 정규화------------------->underfitting 을 막기 위해
4. DropOut 기법------------------------>overfitting을 막기 위해
5. 기타 방법 ( 이미지 한 장을 회전, 밝기, 반전을 시켜서 여러개의 이미지를
만들어서 학습을 시키는 방법 )
"학습이 잘 되도록 데이터를 생성하는 방법"
■ 1. 고급 경사 감소법들
1. SGD
2. Momentum
3. Adagrade
4. Adam
■ 1. SGD (Stochastic Gradient Descent)
확률적 경사 감소법
딥러닝 면접문제:
GD(Gradient Descent) 의 단점은 무엇인가?
1. 학습 데이터를 다 입력해서 한 걸음 이동하므로
시간이 많이 걸린다
그래서 이 문제를 해결하기 위해 나온 것이 ?
SGD(Stochastic Gradient Descent)확률적 경사 감소법
2. 기울기가 global minima 쪽으로 기울어진 방향이 아니기 때문에
global minima 쪽으로 가지 못하고 local minima 에 빠지는 단점이 있다.
예: 구글에 아래의 식의 그래프를 그리시오 !
z = x^2/20 + y^2



global minima 쪽으로 기울기 방향이 있는게 아니기 때문에
local minima 에 빠지고 global minima 쪽으로 가지 못하는 단점이 있다.
SGD의 단점을 해결한 경사 감소법?
■ 2. momentum(운동량)
기존 SGD : 가중치 <--- 가중치 - 러닝레이트 * 기울기
momentum : W <--- W + v(속도)
가중치 <--- 가중치 + v
속도<------- 0.9 * 속도 - 러닝레이트 * 기울기
***0.9 는 마찰계수(알파)
↑
물체가 아무런 힘을 받지 않을 때 서서히 하강시키는 역할을 한다.
물리에서의 지면 마찰이나 공기저항에 해당한다.
내리막: 기울기 음수이면 속도가 증가
오르막: 기울기 양수이면 속도가 감소
기울어진 방향으로 물체가 가속되는 관성의 원리를 적용!
※관성 : 정지해 있는 물체는 계속 정지해 있으려 하고
운동하는 물체는 계속 운동하려는 성질
(예: 100미터 달리기 결승점에서 갑자기 멈춰지지 않는 현상)
즉 가중치에 속도를 붙여서 local minima 를 빠져나온다 !

알파: 마찰계수 (ex: 공기저항력)
■ 3. Adagrade 경사 감소법
"러닝 레이트(학습률)가 신경망 학습이 되면서 자체적으로 조정이 되는
경사 감소법"

SGD vs Adagrade
∂L ∂L ∂L
W<- W-n*---- h<-- h + ----- ◎ ----
∂W ∂W ∂W
*◎는 내적아니고, 원소별 곱셈을 의미
그래서 제곱값이 나온다.
-> 기울기의 제곱값
1 ∂L
W <-- W-n * --------- x ---------
√h ∂W
1. 처음에는 학습률이 크다가 조금씩 감소
2. ◎는 행렬의 원소별 곱셈을 의미하는데
h의 원소가 각각의 매개변수 원소 변화량에
의해 결정된다.
↓
"각각의 매개변수 원소가 갱신되는 값이 다르다"
↓
"많이 움직인 원소일 수록 누적 h의 값이 크니까
갱신되는 정도가 그만큼 감소한다"
**개별맞춤 running rate
■ 4. Adam 경사 감소법
"Momentum의 장점 + Adagrade의 장점을 살린 경사 감소법"
(가속도 이용) (각 매개변수마다 학습률 조정)
최근 딥러닝에서 가장 많이 사용하는 최적화 방법

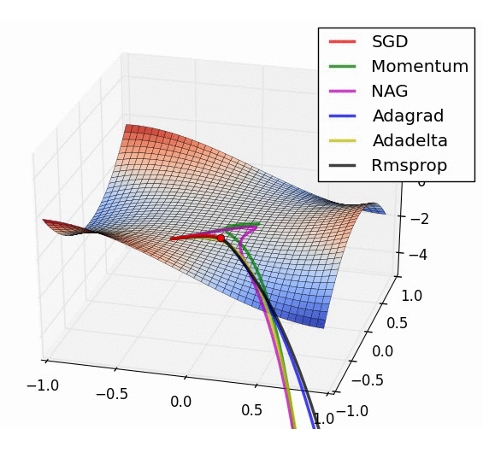
Adadelta = Adam 이 가장 빠르다.
문제239.(점심시간 문제)
어제만든 오차역전파 3층 신경망에 SGD 경사감소를 입히고 학습시켜보시오
191p 의 SGD 클래스 참고
힌트:
class SGD:
def __init__(self, lr = 0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in ('W1', 'b1', 'W2', 'b2', 'W3', 'b3'):
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params,grads)
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
optimizer = SGD() #SGD 클래스를 객체화 시킨다.
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
class TwoLayerNet:
def __init__(self, input_size, hidden_size, hidden_size2, output_size, weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size2)
self.params['b2'] = np.zeros(hidden_size2)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size2, output_size)
self.params['b3'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x) #순전파 태움
y = np.argmax(y, axis=1) #행의 최대값 컴온
if t.ndim != 1: t = np.argmax(t, axis=1) #1차원 아니면 행의 최대값 갖고와라
accuracy = np.sum(y == t) / float(x.shape[0]) # 일치하는거 accuracy로 변수지정
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
grads['W3'] = numerical_gradient(loss_W, self.params['W3'])
grads['b3'] = numerical_gradient(loss_W, self.params['b3'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db # w랑 b를 뽑아서 기울기 구함
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
grads['W3'], grads['b3'] = self.layers['Affine3'].dW, self.layers['Affine3'].db
return grads
class SGD:
def __init__(self, lr = 0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, hidden_size2=30,output_size=10)
optimizer = SGD()
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0] # 60000 개
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num): # 10000
# 미니배치 획득 # 랜덤으로 100개씩 뽑아서 10000번을 수행하니까 백만번
batch_mask = np.random.choice(train_size, batch_size) # 100개 씩 뽑아서 10000번 백만번
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params,grads)
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss) # cost 가 점점 줄어드는것을 보려고
# 1에폭당 정확도 계산 # 여기는 훈련이 아니라 1에폭 되었을때 정확도만 체크
if i % iter_per_epoch == 0: # 600 번마다 정확도 쌓는다.
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc) # 10000/600 개 16개 # 정확도가 점점 올라감
test_acc_list.append(test_acc) # 10000/600 개 16개 # 정확도가 점점 올라감
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
#########################

train acc, test acc | 0.843233333333, 0.8452
문제240.
경사감소법의 종류를 momentum으로 바꿔서 위의 3층 신경망을 학습시키고
속도,정확도를 SGD와 비교하시오
#optimizer = SGD()
optimizer = Momentum()

class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
##############################
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params,grads)
train acc, test acc | 0.9789, 0.9673
문제241. Adagrade 경사감소법으로 위의 3층 신경망을 학습시키시오
class AdaGrad:
def __init__(self,lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, hidden_size2=30,output_size=10)
optimizer = AdaGrad()
train acc, test acc | 0.9434, 0.9366

※정확도 정리
SGD 정확도?
train acc, test acc | 0.843233333333, 0.8452
Momentum 정확도?
train acc, test acc | 0.9789, 0.9673
AdaGrad 정확도?
train acc, test acc | 0.9434, 0.9366
문제242. Adam 경사감소법을 사용한 위의 3층 신경망을 구현하시오
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
optimizer = Adam()
train acc, test acc | 0.9831, 0.9676

hidden_size2 를 100 으로 바꾸니까 adam 99% 나옴

■ 신경망 학습을 높이는 방법
1. 경사 감소법을 SGD 말고 다른 경사감소법으로 수행
2. 가중치 초기화 값 설정
3. 배치 정규화
4. DropOut
■ 2. 가중치 초기화 값 설정
"가중치 초기값을 적절히 설정하면 각 층의 활성화 값의 분포가
적당히 퍼지는 효과가 발생한다.
적당히 퍼지게 되면 학습이 잘되고 정확도가 높아진다."

*이렇게 적당히 퍼져있어야 신경에서는 가장 이상적인 그래프다.
1. 표준편차가 작을수록 delta 가 평균에 가깝게 분포
(시험문제 쉬우면 학생들 점수가 평균에 가깝다)
구현 예: 0.01 * np.random.randn(10, 100)

*신경망에서는
이렇게 평균에 집중되어 있는 현상도 바람직하지 못하다.
다수의 뉴런이 거의 같은 값을 출력하고 있으니 뉴런을 여러 개 둔 의미가
없어진는 뜻이다.
2. 표준편차가 클수록 data가 더 많이 흩어져있다.
(시험문제가 어려우면 아주 잘하는 학생들과 아주 못하는 학생들로
점수가 나눠진다)
구현 예: 1 * np.random.randn(10, 100)

**극과 극으로 나뉘어진 그래프

※바람직한 가중치 초기화값 구성을 위한 방법 2가지
1. Xavier(사비에르) 초기값 구성
표준편차가 1/√n 인 정규 분포로 초기화 한다
(n은 앞층의 노드 수)
구현예:
1/np.sqrt(50) * np.random.randn(10,100)
2. He 초기값 선정
표준편차가 √2/n 인 정규 분포로 초기화 한다
(n은 앞층의 노드 수)
구현예:
np.sqrt(2/50) * np.random.randn(10,100)
■ 가중치 초기화값 설정
1. Xavier -----> sigmoid 함수와 짝꿍
2. He ---------> Relu 함수와 짝꿍
문제243.
우리가 가지고 있는 3층 신경망에 가중치 초기화를 He를 써서 구현하고
정확도를 확인하시오
(현재 Relu 함수로 설정되어있으니 He를 먼저 씁시다)
기존 가중치 초기화값: weight_inti_std = 0.01
변경된 가중치 초기화값: weight_init_std = np.sqrt(2/50)
class TwoLayerNet:
def __init__(self, input_size, hidden_size, hidden_size2, output_size, weight_init_std=np.sqrt(2/50) ):
경사감소법: Adam 사용
train acc, test acc | 0.9956, 0.9709
*overfitting이 약간 일어났다.(테스트값보다 훈련값이 더 높음)
■ 오버피팅을 억제하는 방법 2가지
1. 드롭아웃(DropOut) 책219페이지
2. 가중치 감소(Weight Decay)
■ 드롭아웃(DropOut) "하용호 PPT"
"오버피팅을 방지하기위해서
학습시킬 때 일부러 정보를 누락시키거나 중간중간 노드를 끈다."

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
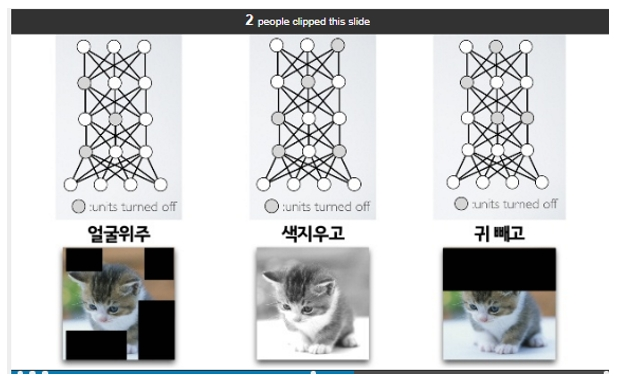
"DropOut 으로 일부에 집착하지 않고
중요한 요소가 무엇인지 터득해 나간다"

# * Dropout class 구현 코드
class Dropout:
"""
http://arxiv.org/abs/1207.0580
"""
def __init__(self, dropout_ratio=0.15):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
#######################################################
※ 설명:
* dropout 클래스의 키가 되는 부분
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
↓
0.15
# 0.15 보다 큰것만 남겨둬라(mask 시켜라)
# 85% 만 남겨두고 15%의 노드는 삭제하겠다 라는 뜻
# 사진의 일부를 없애고 학습시키겠다
# 그러나, 너무 많이 삭제하면 정확도가 떨어지니 주의할 것(underfitting발)
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Dropout1'] = Dropout()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Dropout2'] = Dropout()
train acc, test acc | 0.97165, 0.9604
↓
dropout 없이 Adam 만 돌렸을 때 비하면
학습과 테스트의 차가 줄어들었음을 볼 수 있다.

2. 가중치 감소(Weight Decay)
"학습과정에서 큰 가중치에 대해서는 그에 상응하는 큰 패널티를
부여하여 오버피팅을 억제하는 방법"
예:
고양이와 개사진을 구분하는 신경망
입력층 은닉층
○------>귀가있어요------------->가중치 출력
고양이 ○------> 꼬리가있어요---------->아주 큰 가중치 출력
○-----> 집게발을 가지고있어요->가중치 출력
○-----> 장난스럽게 보여요------> 가중치 출력
*위와같이 학습이 되면 꼬리가 없는 고양이 사진을 입력할 때
고양이가 아니라고 판단한다.
↓해결방법
"가중치 감소(weight decay)"
입력층 은닉층
○------>귀가있어요------------->가중치 출력
고양이 ○------> 꼬리가있어요---------->아주 큰 가중치 출력<-큰패널티
○-----> 집게발을 가지고있어요->가중치 출력
○-----> 장난스럽게 보여요------> 가중치 출력
큰 패널티는 오차함수가 준다.
오차함수가 오차를 역전파 시킬 때 패널티를 부여하게끔 하는데
오차함수 코드가 아래와 같다.
■ 가중치 decay 코드 분석
1
"모든 가중치의 각각의 손실 함수에 --- x 람다 x w^2 을 더한다.
2
1. 오차 함수의 코드에서 수정해야 할 부분
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)
return self.lastLayer.forward(y,t) + wight_decay
↓
오차
2. gradient Descent 업데이트 과정에서 그동안 오차 역전파법에
따른 결과에 정규화 항을 미분한 값에 람다 * 가중치를 더한다.
코드예제:
기존 코드 : grad['W1'] = 미분값
변경된 코드 : grad['W1'] = 미분값 + 람다 * 현재의 가중치
# L2 정규화 적용 후
self.weight_decay_lambda = 0.001 <--- __init__ 에 추가해야할 인스턴스 변수
def loss(self, x, t): # x : (100, 1024), t : (100, 10)
y = self.predict(x) # (100, 10) : 마지막 출력층을 통과한 신경망이 예측한 값
weight_decay = 0
for idx in range(1, 6):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.lastLayer.forward(y, t) + weight_decay
문제244.(오늘의 마지막 문제)
우리가 가지고있는 신경망에 가중치 decay 를 적용해서
오버피팅이 덜 발생하는지 확인하시오

# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
class Dropout:
"""
http://arxiv.org/abs/1207.0580
"""
def __init__(self, dropout_ratio=0.15):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
# 0.15 보다 큰것만 남겨둬라(mask 시켜라)
# 85% 만 남겨두고 15%의 노드는 삭제하겠다 라는 뜻
# 사진의 일부를 없애고 학습시키겠다
# 그러나, 너무 많이 삭제하면 정확도가 떨어지니 주의할 것(underfitting발)
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
class TwoLayerNet:
def __init__(self, input_size, hidden_size, hidden_size2, output_size, weight_init_std=np.sqrt(2/50) ):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, hidden_size2)
self.params['b2'] = np.zeros(hidden_size2)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size2, output_size)
self.params['b3'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Dropout1'] = Dropout()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Dropout2'] = Dropout()
self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])
self.lastLayer = SoftmaxWithLoss()
self.weight_decay_lambda = 0.001
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t): # x : (100, 1024), t : (100, 10)
y = self.predict(x) # (100, 10) : 마지막 출력층을 통과한 신경망이 예측한 값
weight_decay = 0
for idx in range(1, 4): #3층 신경망이라서
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.lastLayer.forward(y, t) + weight_decay
def accuracy(self, x, t):
y = self.predict(x) #순전파 태움
y = np.argmax(y, axis=1) #행의 최대값 컴온
if t.ndim != 1: t = np.argmax(t, axis=1) #1차원 아니면 행의 최대값 갖고와라
accuracy = np.sum(y == t) / float(x.shape[0]) # 일치하는거 accuracy로 변수지정
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
grads['W3'] = numerical_gradient(loss_W, self.params['W3'])
grads['b3'] = numerical_gradient(loss_W, self.params['b3'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db # w랑 b를 뽑아서 기울기 구함
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
grads['W3'], grads['b3'] = self.layers['Affine3'].dW, self.layers['Affine3'].db
return grads
class SGD:
def __init__(self, lr = 0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
class AdaGrad:
def __init__(self,lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, hidden_size2=100,output_size=10)
optimizer = Adam()
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 적절히 설정한다.
train_size = x_train.shape[0] # 60000 개
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num): # 10000
# 미니배치 획득 # 랜덤으로 100개씩 뽑아서 10000번을 수행하니까 백만번
batch_mask = np.random.choice(train_size, batch_size) # 100개 씩 뽑아서 10000번 백만번
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params,grads)
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss) # cost 가 점점 줄어드는것을 보려고
# 1에폭당 정확도 계산 # 여기는 훈련이 아니라 1에폭 되었을때 정확도만 체크
if i % iter_per_epoch == 0: # 600 번마다 정확도 쌓는다.
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc) # 10000/600 개 16개 # 정확도가 점점 올라감
test_acc_list.append(test_acc) # 10000/600 개 16개 # 정확도가 점점 올라감
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
##########################################################
■ 신경망 학습을 잘되게 하기 위한 방법들을 소개
-underfitting 을 줄이기 위한 방법들?
1. 가중치 초기화 값 선정( Xavier( sigmoid ), He( relu ) )
*각 층의 활성화 분포 고르게 !
2. 경사감소법의 종류(SGD, momentum, adagrad, adam)
*관성이용: mementum
*가중치 자동조절: adagrad
*위 2개 합친 것: adam
3. 배치정규화
-overfitting 을 줄이기 위한 방법들?
1. DropOut
2. Weightdecay
■ 배치정규화(p210)
↓
"batch normalization"
batch 단위로 가중치의 값을 정규화 하겠다.
통계분석에서 중요한 2가지
1. 표준화 : 평균을 기준으로 얼마나 떨어져 있는지를 나타낸 값
2개 이상의 대상이 단위가 다를 때 대상 데이터를 같은 기준으로
볼 수 있게 해준다.
예: 키와 몸무게는 단위가 다른데 우리반 학생들의 키를 0~1 사이의
숫자로 변경하고 몸무게도 0~1사이 숫자로 변경하면
키와 몸무게 간의 어떤 관계가 있는지 분석을 해볼 수 있다.
|
177(키) |
84(몸무게) |
수식 : (요소값 -평균) / 표준편차
2. 정규화 : normalization. 정규화는 전체 구간을 0~100 으로 설정하여 데이터를
관찰하는 방법이다.
이 방법은 데이터 군에서 특정 데이터가 가지는 위치를 볼 때
사용한다.
예: 우리반에서 내 몸무게 77이면 0~100 사이에 몇 에 해당 되는지
파악이 된다.
수식: (요소값 - 최소값) / (최대값 - 최소값)
문제245.
*****csv파일이 콤마로 나눠줘야 된다. (어떤건 슬래시로 구분되어있어서
인식못함)
우리반의 이름과 나이 데이터를 이용해서 표준화를 시도해서
나의 나이가 0~1 사이 중 어느 부분에 해당 되는지 파이썬으로
확인하시오 !
(요소값 - 평균)/표준편차
답:
# -*- coding: utf-8 -*-
import csv
import numpy as np
file = open('D:\\emp7.csv','r')
#print(file)
emp2_csv = csv.reader(file)
x2 =[]
for emp2_list in emp2_csv:
x2.append(int( emp2_list[1] ))
x3 = np.array(x2)
print( (x3-x3.mean())**2 / x3.std())
[ 9.10290536e-01 1.64833053e-01 1.64833053e-01 1.64833053e-01
9.10290536e-01 1.64833053e-01 2.01920490e-02 3.19116791e+00
2.01920490e-02 1.64833053e-01 2.25656450e+00 9.10290536e-01
6.75156185e+00 9.10290536e-01 9.10290536e-01 2.25656450e+00
4.20365494e+00 9.10290536e-01 3.19116791e+00 4.51481853e+01
2.01920490e-02 1.53335948e+00 8.30923420e+00 1.64833053e-01
5.44979282e+00 1.64833053e-01 9.10290536e-01]
이름까지 나오게
import csv
import numpy as np
file = open('D:\\emp7.csv','r')
#print(file)
emp2_csv = csv.reader(file)
age =[]
ename = []
for emp2_list in emp2_csv:
age.append(int( emp2_list[1] ))
ename.append(emp2_list[0])
age=np.array(age)
age_m = (age-age.mean())**2 / age.std()
for i, j in zip(ename, age_m):
print(i,j)
서일 0.910290535501
엄한솔 0.164833053056
김준구 0.164833053056
문제246.
우리반 나이 데이터를 가지고 정규화(normalization)을 해서
나이를 0~100 사이의 숫자로 나타내시오
수식: (요소값 - 최소값) / (최대값 - 최소값)
# -*- coding: utf-8 -*-
import csv
import numpy as np
file = open('D:\\emp7.csv','r')
emp2_csv = csv.reader(file)
#print(emp2_csv)
x2 =[]
for emp2_list in emp2_csv:
x2.append(int(emp2_list[1]))
x3 = np.array(x2)
print( ( x3 - x3.min()) / (x3.max() - x3.min()))
[ 0.17647059 0.23529412 0.23529412 0.23529412 0.17647059 0.23529412
0.29411765 0.47058824 0.29411765 0.23529412 0.11764706 0.17647059
0. 0.17647059 0.17647059 0.11764706 0.05882353 0.17647059
0.47058824 1. 0.29411765 0.41176471 0.58823529 0.23529412
0.52941176 0.23529412 0.17647059]
가중치 초기값이 너무 작거나 너무 크면 극단적으로 몰리는 가중치값을 얻게된다.
※바람직한 가중치 초기화값 구성을 위한 방법 2가지
1. Xavier(사비에르) 초기값 구성
2. He 초기값 선정
그런데
문제는 처음에는 데이터가 적절히 분포가 되었다가
점점 학습이 진행되면서 다시 데이터의 분포가 평균에 몰리거나
아니면 아주 잘하거나 아주 못하는 현상이 발생하게 된다.
즉 학습이 진행될 수록 분포가 틀어지는 현상이 생긴다.
그래서 배치 정규화를 통해서 각 층의 활성화 값이 적당히 분포되도록
강제로 조정할 필요가 있는데 그게 배치 정규화 이다.

배치 정규화를 신경망에 적절히 삽입해 주면 된다.
배치 정규화는 활성화 함수 앞이나 뒤쪽에 입력할 수 있지만
대게는 활성화 함수 앞에 사용한다.
■ 배치 정규화 공식
p211
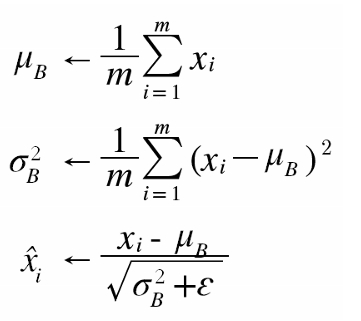
첫번째 식: 뮤 (평균 구하는 식) m은 미니배치값
두번째 식: (분산 구하는 식)
세번째 식: (표준편차 구하는 식)
아주작은값의 입실런을 더하는 이유 -> 0으로 수렴 방지
↑
정규화 시켜주는 것
*표준화는 표본뽑아 구하는 것.
*공식은 정규화 공식이나, 미니배치가 표본값이라 결국 구하는 값은 표본값이다.
배치 정규화는 기본적으로 데이터 분포가 평균이 0, 분산이 1이 되도록
정규화한다.
사이즈가 m인 미니배치에 대하여 평균과 분산을 구한다.
그리고 이 입력 데이터를 평균이 0 , 분산이 1이 되도록 정규화를 한다.
■ 배치 정규화의 장점( p210)
1. 학습을 빨리 진행할 수 있다.(언더피팅도 해결된다)
2. 초기값에 크게 의존하지 않아도 된다.(역시 언더피팅 해결)
3. 오버피팅을 억제한다.
이 입력 데이터를 평균이 0, 분산 1 이 되도록 정규화를 하는데
그런데 신경망은 비선형을 가지고 있어야
표현력이 커져 복잡한 함수를 표현할 수 있는데
위와 같이 평균이 0, 분산을 1로 고정시키는 것은 활성화 함수의
비선형을 없애버릴 수 있다.
그래서
아래와 같이 감마와 베타를 이용해서 새로운 값을 내놓는다.

감마가 데이터의 확대(분포)를 조정하는 것이고
베타가 데이터의 이동을 조정하는 것인데 학습이 되면서
감마와 베타가 자동으로 신경망에 맞게 조정이 된다.
■ 배치 정규화의 계산 그래프

문제247.(점심시간 문제)
위의 배치 정규화 계산 그래프 forward 함수를 생성하시오
(입력값 우리반 나이 데이터)
import csv
import numpy as np
file = open('D:\\emp7.csv','r')
emp2_csv = csv.reader(file)
age=[]
ename=[]
for emp2_list in emp2_csv:
age.append(int( emp2_list[1] ))
ename.append(emp2_list[0])
age = np.array(age)
def batch_noarm_forward(x , gamma, beta, eps):
#식 6.7 구현
m = x.mean()
val = x.var() #var() 쓰면 분산 바로 구해짐
xx = (x-m)/np.sqrt(val + eps) # x에 맞춰서 브로드캐스트 됨
return gamma*xx + beta
#식 6.8 구현
x = age
print( batch_noarm_forward( x, 1, 0, 0.01 ) )
[-0.52269706 -0.22242428 -0.22242428 -0.22242428 -0.52269706 -0.22242428
0.0778485 0.97866684 0.0778485 -0.22242428 -0.82296984 -0.52269706
-1.4235154 -0.52269706 -0.52269706 -0.82296984 -1.12324262 -0.52269706
0.97866684 3.68112185 0.0778485 0.67839406 1.57921239 -0.22242428
1.27893961 -0.22242428 -0.52269706]
■ 배치 정규화의 역전파
참고사이트

문제248.
아래의 코드를 이용해서 우리가 가지고 있는 3층 신경망에 배치 정규화코드를
추가하시오
layer함수 이미 배치정규화 함수가 있음. 그거 가져와서 쓰면 됨
BatchNormalization(gamma, beta)
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['BatchNorm1'] = BatchNormalization(gamma=1.0, beta=0.)
self.layers['Relu1'] = Relu()
self.layers['Dropout1'] = Dropout()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.layers['BatchNorm2'] = BatchNormalization(gamma=1.0, beta=0.)
self.layers['Relu2'] = Relu()
self.layers['Dropout2'] = Dropout()
96, 95% 나왔음.
dropout 빼고 돌리면
99% 나옴!!
'deeplearning' 카테고리의 다른 글
| 7장. 합성곱 신경망(CNN) (0) | 2019.03.30 |
|---|---|
| 5장. 오차 역전파 ( 계산 그래프, 연쇄법칙, 역전파 ) (0) | 2019.03.27 |
| 4장. 인공 신경망을 학습시킴(손실(오차)함수, 수치 미분, 경사하강법, 학습 알고리즘 구현) (0) | 2019.03.27 |
| 3장. 인공 신경망 ( 신경망의 활성화 함수, 3층 신경망 구현 ) (0) | 2019.03.27 |
| 2장. 퍼셉트론Perceptron (0) | 2019.03.27 |



