■회귀트리

1) 회귀트리란?
수치를 예측하는 트리(종속변수가 양적변수 일 경우)
2) 특정 숫자를 예측하는데 다중 회귀분석을 이용하지 않고
왜 회귀트리를 사용하는가?
예측해야 하는 특정 숫자(집값) <-- 평 수, 학군, 지하철과의 거리...
와인의 등급 <-- 휘발성, 알콜함량, 자유이산화황


수치예측 작업을 할 때 일반적으로 전통적인 회귀방법을
가장 먼저 선택하지만,
경우에 따라 수치 의사 결정트리가 분명한 이점을 제공하기도 한다.
예를 들어 의사결정트리의 장점을 수치예측에 활용할 수 있다.
의사결정트리는 작업이 특징이 많거나 결과간에 매우 복잡하고
비선형적인 관계를 가질 때 잘 맞는 반면, 회귀는 이럴 때
어려움이 있다.
회귀의 경우 독립변수의 갯수가 많으면 다중공선성과 결정계수를
높이기 위해 파생변수를 추가해야 하는 작업들이 필요했다.
3) 회귀트리
선생님 주신 회귀트리 PPT
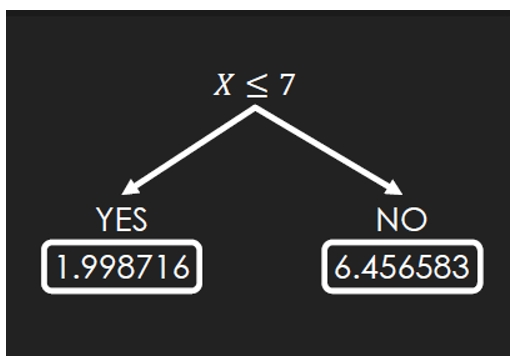
4) SDR 테스트

속성 A와 B 중에 어떤 것이 다 균일하게 나누었는지 SDR 을 확인한다.
tee<-c(1,1,1,2,2,3,4,5,5,6,6,7,7,7,7)
at1<-c(1,1,1,2,2,3,4,5,5)
at2<-c(6,6,7,7,7,7)
bt1<-c(1,1,1,2,2,3,4)
bt2<-c(5,5,6,6,7,7,7,7)
SDR_func<-function(total, a1, a2){
return( sd(total) - (length(a1)/length(total)*sd(a1)+
length(a2)/length(total)*sd(a2) ) )
}
> SDR_func(tee,at1, at2)
[1] 1.202815
> SDR_func(tee, bt1, bt2)
[1] 1.392751
SDR_B 가 1.39로 더 높으니 b속성으로 나누는 것을 결정하고
각각 bt1, bt2 평균값을 구해서 등급을 예측하자.
mean(bt1)
[1] 2
> mean(bt2)
[1] 6.25
■ 와인 품질 평가 예측 모델 만들기
■ 회귀 트리 (Regression Tree)
1. 와인 데이터에 대한 소개
■ 와인 데이터로 의사결정 트리 시각화
#fixed.acidity : 고정 산도
#volatile.acidity : 휘발성 산도
#citric.acid : 시트르산
#residual.sugar : 잔류 설탕
#chlorides : 염화물
#free.sulfur.dioxide : 자유 이산화황
#total.sulfur.dioxide: 총 이산화황
#density : 밀도
#pH : pH
#sulphates : 황산염
#alcohol : 알코올
#quality : 품질
wine <- read.csv("whitewines.csv")
2. 와인의 quality 데이터가 정규분포에 속하는 안정적인
데이터 인지 확인
hist(wine$quality)

3. wine 데이터를 train 데이터와 test 데이터로 나눈다.
wine_train <- wine[1:3750, ]
wine_test <- wine[3751:4898, ]
4. train 데이터를 가지고 model 을 생성한다.
library(rpart)
#의사결정나무를 만드는 다양한 패키지 중 하나인 rpart
model <- rpart( quality ~ . , data=wine_train)
model
model
n= 3750
node), split, n, deviance, yval
* denotes terminal node
1) root 3750 2945.53200 5.870933
2) alcohol< 10.85 2372 1418.86100 5.604975
4) volatile.acidity>=0.2275 1611 821.30730 5.432030
8) volatile.acidity>=0.3025 688 278.97670 5.255814 *
9) volatile.acidity< 0.3025 923 505.04230 5.563380 *
5) volatile.acidity< 0.2275 761 447.36400 5.971091 *
3) alcohol>=10.85 1378 1070.08200 6.328737
6) free.sulfur.dioxide< 10.5 84 95.55952 5.369048 *
7) free.sulfur.dioxide>=10.5 1294 892.13600 6.391036
14) alcohol< 11.76667 629 430.11130 6.173291
28) volatile.acidity>=0.465 11 10.72727 4.545455 *
29) volatile.acidity< 0.465 618 389.71680 6.202265 *
15) alcohol>=11.76667 665 403.99400 6.596992 *
5. 위에서 나온 모델로 트리를 시각화 하시오 !
library(rpart.plot)
rpart.plot( model, digits=3)

rpart.plot(model, digits=3, fallen.leaves=T, type=3, extra=101)
6. 위에서 만든 모델로 테스트 데이터의 라벨을 예측하시오 !
result <- predict(model, wine_test)
7. 테스트 데이터의 실제 라벨(품질) 과 예측결과(품질) 을 비교한다
cbind( round(result), wine_test$quality)
head(cbind( round(result), wine_test$quality))
[,1] [,2]
3751 7 6
3752 5 5
3753 6 6
3754 6 6
3755 6 5
3756 7 7
*6개중 4개 맞추는 걸 눈으로 확인할 수 있다!
8. 테스트 데이터의 라벨과 예측 결과와 상관관계가 어떻게 되는지
확인한다.
cor(result, wine_test$quality)
cor(result, wine_test$quality)
[1] 0.5369525
※ 설명 : 0.53은 두 데이터간의 연관 강도만 측정하는것이다.
그래서 두 데이터간의 오차율이 어떻게 되는지 확인해서
이 오차율을 줄여나가겠금 모델을 튜닝을 한다.
9. 두 데이터간의 오차율을 확인
MAE <- function( actual, predicted) {
mean( abs( actual - predicted) )
}
MAE(result, wine_test$quality)
#result 는 위에서 만든 predict 값!
0.58 <--- 이 모델의 경우 다른 모델인 서포트 벡터 머신에서의
오차는 0.45 인데 0.58이면 상대적으로 좀 큰 오차이
므로 개선의 여지가 필요하다.
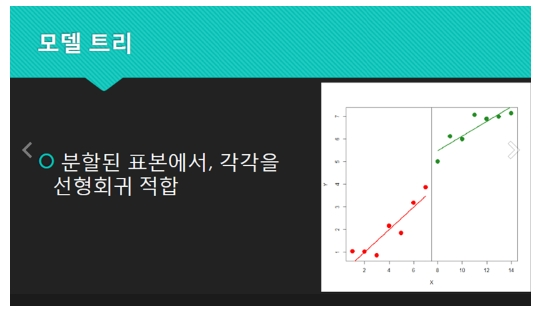
개선방법이 회귀트리 ----> 모델트리로 변경해서 개선을 한다.
분할한 후에 평균값 대신 회귀식을 이용해서 수치를 예측한다
1) 위의 방법 1~3번까지 반복한다
2) 모델트리를 구현하기 위한 패키지 설치
3) 와인의 품질을 예측하는 모델을 생성한다
4) 만든 모델과 테스트 데이터로 예측을 한다
5) 예측값(p.m5p) 과 테스트 데이터의 라벨간의 상관관계를 확인한다
6) 예측값(p.m5p)과 테스트 데이터의 라벨간의 평균절대오차를 확인한다
install.packages("RWeka")
library(RWeka)
m.m5p<- M5P(quality~., data=wine_train)
summary(m.m5p)
summary(m.m5p)
=== Summary ===
Correlation coefficient -0.2222
Mean absolute error 124.1163
Root mean squared error 165.4731
Relative absolute error 18429.7475 %
Root relative squared error 18670.7196 %
Total Number of Instances 3750
p.m5p<- predict(m.m5p, wine_test)
cor(p.m5p, wine_test$quality)
MAE <- function( actual, predicted) {
mean( abs( actual - predicted) )
}
MAE(wine_test$quality, p.m5p)
MAE(wine_test$quality, p.m5p)
[1] 122.4056
문제240. 보스턴 하우징 데이터( 보스턴 지역의 집값) 을 이용해서 \
회귀트리 모델을 생성하시오 !
범죄율, 방의 갯수, 지역의 학교의 교사의 숫자,
강과 인접한 거리등의 데이터를 확인해서 회귀트리 생성
(라벨 : MEDV(집값),
cat.MEDV (주택가격이 3만달러가 넘는지 안넘는지에 대한 라벨)

답:
# 데이터를 로드한다.
boston <- read.csv("D:/data/boston.csv")
# 본래 데이터의 최소값, 최대값 비교
summary(boston$MEDV)
# 훈련과 테스트 데이터 생성
boston_train <- boston[1:495, ]
boston_test <- boston[496:506, ]
str(boston_train)
# 회귀트리 모델을 생성한다.
model <- rpart( MEDV ~ . , data=boston_train)
model
# 생성된 모델과 테스트 데이터로 예측한다.
result <- predict(model, boston_test)
# 결과와 실제 테스트 라벨과의 상관정도를 확인한다.
cor(result, boston_test$MEDV)
0.2808209
# 결과와 실제 테스트 라벨과의 평균절대오차를 확인한다.
MAE <- function( actual, predicted) {
mean( abs( actual - predicted) )
}
MAE( result, boston_test$MEDV)
3.484211
# 이번에는 보스톤 하우징 데이터를 모델트리로 구현해서 성능을
높여본다.
library(RWeka)
m.m5p <- M5P(MEDV ~ . , data=boston_train)
p.m5p <- predict( m.m5p, boston_test)
cor( p.m5p , boston_test$MEDV )
0.506185
MAE( boston_test$MEDV, p.m5p)
2.869352


