■ k-means 군집화
- K-means 군집화 이론 수업
- K-menas 군집화 실습1 (국영수 점수)
- K-means 군집화 실습2 (소셜 미이더에 같은 성향을 갖는 사람들을 분류)
*머신러닝의 종류 3가지
- 지도학습 :
- 분류: 의사결정트리, 나이브베이즈, knn
- 회귀: 다중 회귀분석
- 비지도 학습: k-means ---> 정답라벨 없이 기계학습 시키는 학습방법
3. 강화학습
■ 1. k-means 군집화 이론 수업
*k 평균 군집화 알고리즘 이란? (페이퍼21번)
K-평균 알고리즘은 주어진 데이터를 k개의 클러스터로 묶는 알고리즘으로,
각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작한다.
이 알고리즘은 자율학습의 일종으로 라벨이 달려있지않은 입력 데이터에
라벨을 달아주는 역할을 수행한다.
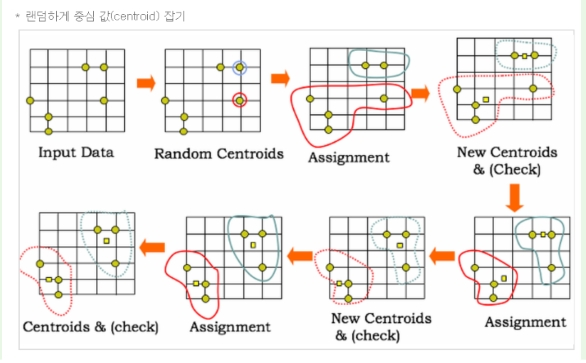
*컴퓨터가 어떻게 클러스터 구성에 대한 사전 지식없이
라벨이 없는 데이터에 군집화를 가능하게 할까?(페이퍼 22번)
클러스터 안에 있는 아이템들은 서로 아주 비슷해야하지만
클러스터 밖에 있는 아이템들과는 아주 달라야 한다는
원칙을 따르면 가능하다(p388)
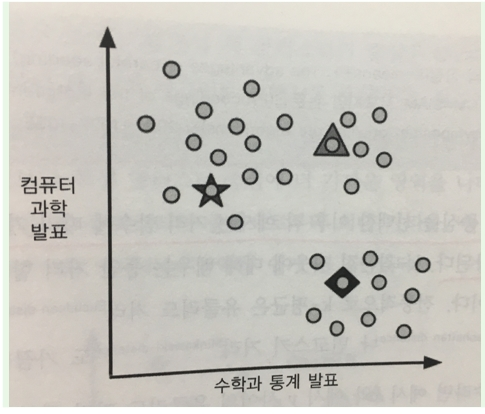
*k평균 알고리즘의 목표가 무엇인가(페이퍼 24번)
클러스터 내의 차이를 최소화하고 클러스터간의 차이를 최대화 하는 것이다.
*knn 과 k-means 의 공통점과 차이점? (페이퍼 25번)
공통점?
거리함수(유클리드 거리)를 이용해서 중심에서 가까운 거리에 있는
데이터를 클러스터링 한다
차이점?
Knn은 라벨(정답)이 있고 k-means는 라벨(정답)이 없다.
■ k-means 기본실습
- 기본 데이터셋을 만든다
- 위에서 만든 데이터 셋으로 plot 그래프를 그린다
- K-means 패키지를 설치한다
- K-means 함수로 데이터를 분류한다
- 분류한 파라미터값 가지고 다시 한번 시각화를 한다
- 원래 데이터로 그린 plot 그래프와 분류한 그래프를 같이 출력한다
예제:
기본 데이터셋을 만든다
c <- c(3,4,1,5,7,9,5,4,6,8,4,5,9,8,7,8,6,7,2,1)
c
row <- c("A","B","C","D","E","F","G","H","I","J")
row
col <- c("X","Y")
col
data <- matrix( c, nrow= 10, ncol=2, byrow=TRUE, dimnames=list(row,col))
data
data
X Y
A 3 4
B 1 5
C 7 9
D 5 4
E 6 8
F 4 5
G 9 8
H 7 8
I 6 7
J 2 1
2. 위에서 만든 데이터셋으로 plot 그래프를 그린다
plot(data)
3. k-means 패키지를 설치한다
install.packages("stats")
#기본 패키지라고 설치나 업데이트가 필요없다고 뜬다.
library(stats)
4. kmeans 함수로 데이터를 분류한다.
※ k 개 구하는 공식 : k=sqrt(n/2) (페이퍼문제29번)
km <- kmeans(data,2)
> km
> km
K-means clustering with 2 clusters of sizes 5, 5
Cluster means: # 각 군집의 중앙 좌표값
X Y
1 7 8.0
2 3 3.8
Clustering vector:
A B C D E F G H I J
2 2 1 2 1 2 1 1 1 2
Within cluster sum of squares by cluster:
[1] 8.0 20.8
(between_SS / total_SS = 74.5 %)
Available components:
[1] "cluster" "centers" "totss" "withinss"
[5] "tot.withinss" "betweenss" "size" "iter"
[9] "ifault"
> km$center # 중앙점이 어딘지 확인한다.
X Y
1 7 8.0
2 3 3.8
> cbind(data, km$cluster)
X Y
A 3 4 2
B 1 5 2
C 7 9 1
D 5 4 2
E 6 8 1
F 4 5 2
G 9 8 1
H 7 8 1
I 6 7 1
J 2 1 2
5. 분류한 파라미터값을 가지고 다시 한번 시각화를
한다.
plot(round(km$center), col=km$center, pch=22,
bg=km$center, xlim=range(0:10),ylim=range(0:10))

6. 원래 데이터를 그린 plot 그래프와 위의 그래프를
합쳐서 출력한다.
plot(round(km$center), col=km$center, pch=22,
bg=km$center, xlim=range(0:10),ylim=range(0:10))
par(new=T)
plot( data, col=km$cluster+1,
xlim=range(0:10), ylim=range(0:10) )

문제253. 위의 data 를 factoextra 패키지를 이용해서 시각화 하시오 !
install.packages("factoextra")
library(factoextra)
km <- kmeans(data,2)
fviz_cluster(km, data = data, stand=F)
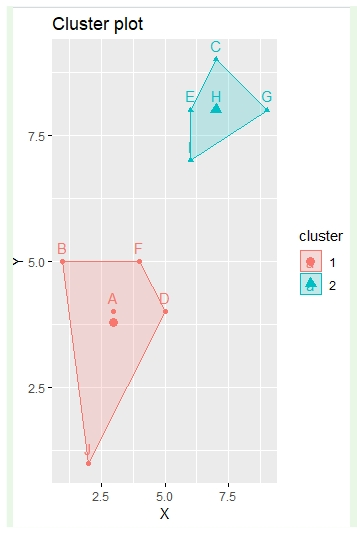


■ k 평균 군집화 실습1 (국영수 점수를 가지고 학생 분류)
문제254.
국영수 점수 데이터를 가지고 k값을 4두고 학생들을 분류하시오
분류하고 시각화도 하시오
(수학점수와 영어점수로만 분류)
1. 수학, 영어 둘 다 잘하는 학생들
2. 수학은 잘하는데 영어를 못하는 학생들
3. 영어는 잘하는데 수학을 못하는 학생들
4. 수학, 영어 둘 다 못하는 학생들
academy<-read.csv("academy.csv")
names(academy)
head(academy)
academy<-academy[, c(3,4)]
head(academy)
수학점수평균 영어점수평균
1 75 85
2 90 60
3 53 48
4 96 62
5 89 80
6 92 90
km<-kmeans(academy,4)
km
K-means clustering with 4 clusters of sizes 13, 12, 17, 10
Cluster means:
수학점수평균 영어점수평균
1 91.38462 83.76923
2 70.00000 84.16667
3 83.05882 64.58824
4 49.40000 54.40000
fviz_cluster(km, data = academy, stand=F)

문제255. 학생번호, 수학점수, 영어점수, 분류번호가 같이 출력되게하시오 !
academy<-read.csv("academy.csv")
head(cbind(academy[ , c(1,3,4)], km$cluster))
head(cbind(academy[ , c(1,3,4)], km$cluster))
학생번호 수학점수평균 영어점수평균 km$cluster
1 1 75 85 2
2 2 90 60 3
3 3 53 48 4
4 4 96 62 3
5 5 89 80 1
6 6 92 90 1
문제256. 미국 대학 입학 점수를 가지고 academic 점수와 sport 점수를
x , y 축으로 두고 4가지 클래스로 분류하시오 !
set.seed(11)
enter_score<-read.csv("sports.csv")
head(enter_score)
enter_score<-enter_score[, c(2,3)]
km<-kmeans(enter_score,4)
fviz_cluster(km, data=enter_score, stand=F)

문제257.
동물 데이터를 가지고 k-means 머신러닝 기법을 수행해서 동물 데이터의 라벨과
k-means 의 클러스터가 일치하는지 확인해보시오 !
머신러닝 데이터 게시판 87 동물 데이터
마지막 컬럼이 라벨
1: 포유류
2 : 조류
3 : 파충류
4 : 어류
5 : 양서류
6 : 곤충
7 : 갑각류
zoo<- read.csv("zoo.csv")
head(zoo)
length(zoo) # 컬럼갯수 ncol 명령어도 됨
zoo_n<-zoo[, 2:17] # 트레인 데이터
head(zoo_n)
zoo_model<- kmeans(zoo_n, 7) # 7개로 kmeans 분류
x<-cbind(zoo[,18], zoo_model$cluster) # 18번쨰를 테스트데이터로.
head(x)
xx<-data.frame(x)
head(xx)
library(doBy)
head(orderBy(~X1, xx))
table(xx$X1, xx$X2)
1 2 3 4 5 6 7
1 0 0 0 7 0 3 30
2 0 20 0 0 0 0 0
3 2 0 2 0 0 1 0
4 0 0 0 0 0 13 0
5 0 0 4 0 0 0 0
6 0 0 0 0 8 0 0
7 4 0 2 0 4 0 0
1: 포유류
2 : 조류
3 : 파충류
4 : 어류
5 : 양서류
6 : 곤충
7 : 갑각류
문제258(점심시간문제)
부도여부 데이터(라벨있는 데이터)를 k-means 머신러닝 기법으로
분류해서 동물 데이터처럼 라벨과 일치하는지 확인해보시오
부도예측데이터3.csv
budo<- read.csv("부도예측데이터3.csv")
head(budo)
ncol(budo) # 44
names(budo)
budo<-budo[,-1] # 43
x<-budo[, 1:42]
km<-kmeans(x, 10)
cluster<-cbind(budo[,43], km$cluster)
head(cluster)
cluster<-data.frame(cluster)
head(cluster)
head(table(cluster$X1, cluster$X2))
head(table(cluster$X1, cluster$X2))
1 2 3 4 5 6 7 8 9 10
-27 0 0 0 1 0 1 0 0 0 0
-25.166 0 0 0 0 0 1 0 0 0 0
-21.875 0 1 0 0 0 0 0 0 0 0
-18.84 0 1 0 0 0 0 0 0 0 0
-14.206 0 0 0 1 0 0 0 0 0 0
-9.447 0 0 0 1 0 0 0 0 0 0
■ k평균 군집화 실습(소개팅 데이터)
like.csv
문제259.
소개팅 데이터를 kmeans 로 분석해서 소개팅했던 상대방의 라벨과
kmeans cluster 와 일치하는지 확인하시오
set.seed(1)
like<-read.csv("like.csv")
ncol(like) # 8
model_like<-like[,-8]
ncol(model_like)
like_km<-kmeans(model_like, 3)
x<-cbind(like[,8], like_km$cluster)
x
x
[,1] [,2]
[1,] 1 2
[2,] 2 3
[3,] 2 3
[4,] 3 1
[5,] 1 2
[6,] 3 1
[7,] 1 2
[8,] 2 3
[9,] 3 1
[10,] 1 2
[11,] 3 1
[12,] 1 2
[13,] 2 3
[14,] 3 1
x2<-data.frame(x)
table(x2)
table(x2)
X1 1 2 3
1 0 5 0
2 0 0 4
3 5 0 0
model_like $ kmeans 3 시킨거
manytalk likebook liketravel grade tall skin muscle
1 30 80 40 40 90 90 50
2 60 50 70 50 60 60 90
3 50 40 80 60 50 70 80
4 90 50 60 30 40 20 30
5 50 70 30 70 70 80 60
6 70 30 60 40 40 40 30
7 40 90 60 60 60 80 60
8 30 60 90 60 40 70 70
9 80 40 20 80 60 40 50
10 50 70 70 50 70 90 50
11 80 50 60 40 50 40 70
12 30 70 30 90 70 80 60
13 40 60 90 60 50 70 80
14 80 30 50 50 80 40 60
data.frame(like$likelabel) # cbind 시킨거에서 X1 값
like.likelabel
1 1타입
2 2타입
3 2타입
4 3타입
5 1타입
6 3타입
7 1타입
8 2타입
9 3타입
10 1타입
11 3타입
12 1타입
13 2타입
14 3타입
■ k-means 군집화 실습(소셜 미디어에 같은 성향을 갖는 사람들을 분류)
■ k평균 군집화 실습2 (소셜 미디어에 같은 성향을 갖는 사람들을 분류)
1. 데이터를 로드한다.
teens <- read.csv("snsdata.csv")
str(teens)
head(teens[,c(1,2,3)])
gradyear gender age
1 2006 M 18.982
2 2006 F 18.801
3 2006 M 18.335
4 2006 F 18.875
5 2006 <NA> 18.995
6 2006 F NA
# 데이터에 성별이 NA로 결측치가 존재한다.
summary(teens$age)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
3.086 16.312 17.287 17.994 18.259 106.927 5086
# age컬럼에도 na 값이 있음을 확인할 수 있다.
2. 성별이 남자가 몇명이고 여자가 몇명인지 확인한다.
# table 이 group 시키는거랑 같은 기능
table(teens$gender)
F M
22054 5222
3. 성별에 NA 가 몇개인지도 출력되게하시오
table(teens$gender, useNA="ifany")
F M <NA>
22054 5222 2724
4. 고등학생 데이터라는 정확한 데이터 분석을 위해서
나이가 13세 ~ 20세 가 아니면 다 NA 처리해라 !
teens$age <- ifelse(teens$age>=13 & teens$age <20,
teens$age, NA)
summary(teens$age)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
13.03 16.30 17.27 17.25 18.22 20.00 5523
*왜 na 값이 늘어났을까?
5. 정확한 데이터 분석을 위해 성별에 관련한 더미변수 2개를
생성한다.
teens$female <- ifelse(teens$gender=="F" & !is.na(teens$gender),
1, 0)
teens$no_gender <- ifelse(is.na(teens$gender),1,0)
table(teens$gender, useNA="ifany")
F M <NA>
22054 5222 2724
table(teens$female, useNA="ifany") #앞서 분류해놔서 useNA 안써도 됨
0 1
7946 22054
table(teens$no_gender, useNA="ifany")
0 1
27276 2724
6. 나이가 결측치로 나온 데이터를 졸업년도로 나이를 추정해서
결측치를 채워넣는 작업
ave_age <- ave(teens$age, teens$gradyear,
FUN=function(x) mean(x, na.rm=TRUE) )
# 결측 측량 및 통계분석(미포함) : na.rm = TRUE
# (), mean(), sd(), min(), max(), range() 등등. 방정식을 계산할 때
# 옵션을 선택하지 않으면 na.rm = TRUE 가 됩니다.
head(teens[,c(1,2,3)])
gradyear gender age
1 2006 M 18.982
2 2006 F 18.801
3 2006 M 18.335
4 2006 F 18.875
5 2006 <NA> 18.995
6 2006 F NA
# 해당 졸업년도의 age를 가지고 데이터 평균내어
# 그 값을 ave_age 에 저장한다.
head(data.frame(ave_age))
ave_age
1 18.65586
2 18.65586
3 18.65586
4 18.65586
5 18.65586
6 18.65586
teens$age <- ifelse( is.na(teens$age), ave_age, teens$age)
#년도별 추정한 평균나이를 teens$age의 na 값에 담는다
summary(teens$age)
Min. 1st Qu. Median Mean 3rd Qu. Max.
13.03 16.28 17.24 17.24 18.21 20.00
7. sns 에 나타났던 관심사 횟수를 표현하는 36개의 수치형 데이터
컬럼을 정규화 시킨다.
interests <- teens[5:40]
interests_z <- as.data.frame(lapply(interests, scale)) # lapply 리스트로 반환
head(interests_z)
8. kmeans 함수로 5개의 클래스로 분류 한다.
set.seed(2345)
teen_clusters <- kmeans(interests_z, 5)
teen_clusters
9. 각 클래스의 갯수가 각각 어떻게 되는지 확인하시오
teen_clusters$size
[1] 871 600 5981 1034 21514
10. 클러스터의 중심점의 좌표를 확인한다
teen_clusters$centers


