■ 모델 성능평가
1. 혼돈행렬을 사용한 성능 척도
2. 카파 통계량
3. 민감도와 특이도
4. 정밀도와 재현률
5. F 척도
6. 성능 트레이드 오프 시각화(Roc 곡선)
7. 홀드아웃
■ 모델 성능 평가가 중요한 이유가 무엇인가?
머신러닝(학생)이 수행한 결과(분류, 예측)에 대한 공정한 평가를
통해 머신러닝(학생)이 앞으로도 미래의 데이터에 대해서 잘 분류하고
예측할 수 있도록 해주고 분류결과가 요행수로 맞힌게 아니다라는 것을
확신하게 해주며 분류결과를 좀 더 일반화 할 수 있기 때문이다.
■ 정확도는 무엇인가?
학습자가 맞거나 틀린 경우의 비율을 나타낸다.
정확도: (TP+TN )/TP+TN+FN+FP
= 100 에서 FP+FN을 뺀 값 또는 "TRUE/전체"
■ 모델 성능 평가를 위해 정확도만으로는 충분하지 않은 이유?
암 판정하는 분류기가 99%의 정확도를 갖고있다고 하면
1%의 오류율이 있기 때문에 어떤 데이터에 대해서는 오류를 범할수도
있게 된다.
그래서 정확도 만으로는 성능을 측정하는데 충분치 않다. 정확도와 더불어서
분류기의 유용성에 대한 다른 성능 척도를 정의하는 것이 중요하다.
"정확도 + 다른 성능 척도"
■ 그럼 다른 성능 척도에는 무엇이 있는가?
1. 카파 통계량
2. 민감도와 특이도
3. 정밀도와 재현률
4. Roc 곡선
■ 이원교차표에서 정확도와 오류율을 확인하는 방법

정확도 = (TP + TN) / (TP+ TN+FP+FN)
문제261.
혼돈행렬을 사용한 성능척도 공식을 알아보고자 한다.
책 431p 의 정확도를 보는 공식을 이용하여 아래의 분류 결과의
정확도와 오류율을 각각 확인하시오
정확도 = (TP + TN) / (TP+ TN+FP+FN)
오류율 = 1-정확도
|
|
ham |
spam |
|
ham |
1203 |
4 |
|
spam |
31 |
152 |
정확도 = 0.974
오류율 = 1-0.974 = 0.026
■ 카파 통계량(435p)
*Cohen's Kappa Coefficient (카파 상관계수) ?
두 관찰자간의 측정 범주값에 대한 일치도를 측정하는 방법이다
- 왜 2명 이냐? 이원교차표라서
Pr(a) - Pr(e)
k = ---------------------
1 - Pr(e)
Pr(a) : 데이터에서 관찰된 2명의 평가자들의 일치 확률(실제일치)
Pr(e) : 2명의 평가자들이 데이터로 부터 계산된 확률적으로
일치할 확률(우연히 일치할 확률, 예상일치)
※ k(카파상관계수) 가 0 이면 완전 불일치이고, 1 이면 완전일치 다.
|
거의 일치하지 않음 |
0.20 보다 적음 |
|
어느 정도 일치 |
0.20 ~ 0.40 |
|
보통 일치 |
0.40 ~ 0.60 |
|
좋은 일치 |
0.60 ~ 0.80 |
|
매우 좋은 일치 |
0.80 ~ 1.00 |
예시: 시험을 응시한 학생이 100명이라고 할 때
2명의 평가자가 합격, 불합격을 각각 판정하고
두 평가자의 일치도를 아래와 같이 보여주고 있다.

※ 설명: 평가자 A와 B 모두 40명에게 합격을, 30명에게 불합격을
주었다. Pr(a)는 2명의 평가자들이 실제 일치할 확률이므로 0.7 이 된다
40 + 30 70
Pr(a) = -------------- = ---------
100 100
Pr(e) 를 계산하기 위해서는 평가자 A와 평가자 B의 각각의 합격과
불합격을 줄 확률을 구해야 한다
전체 100
1. 평가자 A : 합격을 60번, 불합격을 40번 주었다( 0.6, 0.4의 확률 )
2. 평가자 B : 합격을 50번, 불합격을 50번 주었다( 0.5와 0.5의 확률)
평가자 A와 평가자 B 둘 모두 확률적으로 "합격" 을 줄 확률은
0.6 * 0.5 = 0.3 이다.
평가자 A와 평가자 B 둘 모두 확률적으로 "불합격"을 줄 확률은
0.4 * 0.5 = 0.2 이다.
Pr(e) 는 데이터로 부터 계산된 확률적으로 일치할 확률이므로
이 둘을 더해서 0.3 + 0.2 = 0.5 이다.
Pr(a) - Pr(e) 0.7 - 0.5
k = -------------- = ---------- = 0.4
1 - Pr(e) 1 - 0.5
※ k(카파상관계수) 가 0 이면 완전 불일치이고, 1 이면 완전일치 다.
|
거의 일치하지 않음 |
0.20 보다 적음 |
|
어느 정도 일치 |
0.20 ~ 0.40 |
|
보통 일치 |
0.40 ~ 0.60 |
|
좋은 일치 |
0.60 ~ 0.80 |
|
매우 좋은 일치 |
0.80 ~ 1.00 |
*0.4 면 보통일치에 해당하는 걸 볼 수 있다.
문제262.
책 437p 의 이원교차표의 카파 통계량을 계산하시오
|
|
ham |
spam |
|
ham |
1203 |
4 |
|
spam |
31 |
152 |
total: 1390
total ham: 1234
total spam: 156
Pr(a) = (1203 + 152)/1390 = 0.9748
Pr(e)
ham: (1234/1390)=0.8878
spam: (156/1390)=0.1122
ham: (1207/1390)=0.8683
spam: (183/1390)=0.1317
(0.8878*0.8683) + (0.1122*0.1317) = 0.7857
Pr(e) = 0.7857
Pr(a) - Pr(e) 0.9748 - 0.7857
k = -------------- = ------------------- = 0.8787
1 - Pr(e) 1 - 0.7857
|
거의 일치하지 않음 |
0.20 보다 적음 |
|
어느 정도 일치 |
0.20 ~ 0.40 |
|
보통 일치 |
0.40 ~ 0.60 |
|
좋은 일치 |
0.60 ~ 0.80 |
|
매우 좋은 일치 |
0.80 ~ 1.00 |
※ 정확도 뿐만 아니라 kappa 지수도 같이 설명하면서 나온 정확도가
어쩌다 우연히 나온 결과가 아니다 라는 것을 합리적으로
설명할 수 있어야 한다.
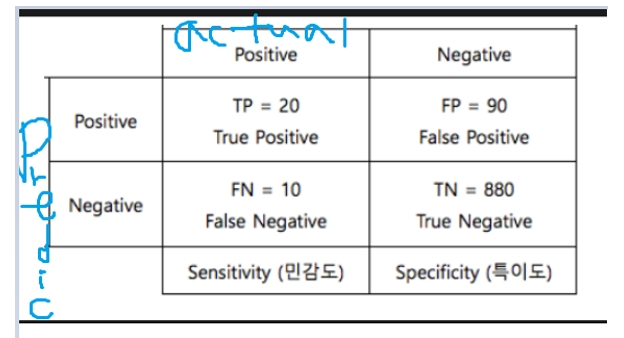
■ 민감도와 특이도(440p)
유용한 분류기를 찾으려면 보통 지나치게 보수적인 예측과
지나치게 공격적인 예측 사이에서의 균형이 필요하다.
보수적인 예측과 공격적인 예측에 대한 것을 정하는 기준이 되는
정보가 민감도와 특이도 이다.

정확도? ( TP + TN ) / Total(=TP+TN+FP+FN)
= ( 20 + 880) / (20+880+90+10) = 0.9
*TRUE 들의 확률
민감도? 실제 참인 것 중에서(actual의 타겟행) 예측"참"=실제"참" 인 확률
= 구매할 것으로 예측한 사람의 구매비율
= TP / (TP+FN)
= 20/(20+10)=0.6667
TP
민감도 =----------
TP + FN
특이도? 실제 거짓인것 중에서 예측"거짓"=실제"거짓"인 확률
= 구매 안할것으로 예측한 사람의 구매 안한 비율
= TN/(TN+FP)
= 880/(880+90)=0.9072
TN
특이도 = ----------
TN + FP

즉, TP와 TN을 잘 맞출 확률이 민감도, 특이도 이다.
민감도와 특이도는 0~1 까지 범위에 있으며 값이 1에 가까울 수록
더 바람직하나 ,
실제로는 한 쪽이 높으면 한쪽이 낮아져서 둘 다 높게 맞출수가 없다
그래서
여러 모델중에 하나를 선택해야 한다면
민감도를 최고로 높게 맞춰놓고 그 중에 특이도 높은 것을 선택한다
민감도가 높으면 특이도가 다소 낮더라도 유용한 모델이라고 볼 수 있는가?
예를들어 예전에 신종플루가 처음 유행했을 때 신속검사를 받아본
사람들은 "이 검사는 정확도가 높지 않으며 추후 2~3일 소요되는
확진검사를 통해 확진판정을 내린다" 는 말을 들어 보았을 것이다
이런 상황이라면 민감도가 높으면 특이도가 다소 낮더라도 가치는
충분하다
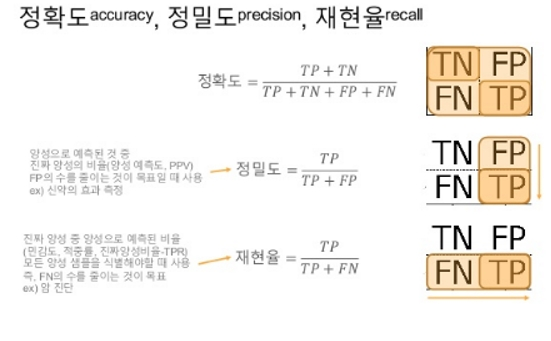
■ 정밀도와 재현율
민감도와 특이도와 긴밀하게 관련된
다른 두 개의 성능 척도인 정밀도와 재현율은
분류에서 만들어진 트레이드오프와 연간돼 있다.
예측이 의미없는 잡음으로 희석됐는지 여부에 대한 징후를 제공하기 위한 것이다.
정밀도 = (예측=실제) / 타겟들
TP
--------- * FP(가장 나쁨) 를 줄이는게 목적인 경우다.
TP + FP
= 예측타겟이
실제와 일치한 비율(스팸으로 예측한 것이 실제 스팸일 비율)
= (예측타겟=실제타겟) / 타겟
TP
재현율 = ----------- * 민감도 공식과 똑같다(예상과 실제가 일치하는 경우)
TP + FN
= 구매 할 것으로 예측한 사람들 중에 구매한 사람의 비율
(민감도와 같다)

1. 소극적 예측: 암이라고 판단하는 것 자체를 소극적으로 봐서
확실한 경우가 아니면 암으로 판단 안 하는것 이다.
정밀도 ↑ , 재현율 ↓
예: 암이 아니라고 예측했는데, 실제로는 암인 경우
병원의 경우는 나쁜 예측이다.
2. 공격적 예측: 조금만 의심이 가도 다 암이라고 판단한다
정밀도↓ , 재현율 ↑
예: 암이 라고 예측했는데, 실제로는 암이 아닌 경우
이 경우는 정밀검사 후 예측이 틀렸어도 괜찮은 경우다.
병원은 공격적 예측을 따르는게 좋다.
문제263.
아래의 스팸/햄 메일을 분류하는 모델의 이원 교차표를 보고
정밀도와 재현율을 각각 구하시오(스팸기준)
예상↓
|
|
ham |
spam |
|
ham |
1203 |
4 |
|
spam |
31 |
152 |
정밀도: 152/(4+152)=0.9744 (타겟의 모든 예상에 대한 맞춘 경우)
재현율: 152/(152+31)=0.8306 (민감도. 실제값이 타겟인 모든 경우)
문제264(점심시간문제)(442p)
스팸/햄 메일을 분류하는 모델의 정밀도와 재현율, 민감도와 특이도를
caret 패키지를 이용해서 구하시오
install.packages("caret")
library(caret)
정밀도
posPredValue(sms_results$predict_type, sms_results$actual_type,
positive = "spam")
0.974359
재현율(=민감도)
민감도
sensitivity(sms_results$predict_type, sms_results$actual_type,
positive = "spam")
0.8306011
특이도
specificity(sms_results$predict_type, sms_results$actual_type,
negative = "ham")
0.996686
문제265.(책 440p 참고)
패키지 irr 을 설치하고 kappa2 함수를 이용해서 스팸/햄 메일 분류 모델의
kappa 지수를 구하시오
install.packages("irr")
library(irr)
kappa2(sms_results[1:2])
Cohen's Kappa for 2 Raters (Weights: unweighted)
Subjects = 1390
Raters = 2
Kappa = 0.883
z = 33
p-value = 0
|
거의 일치하지 않음 |
0.20 보다 적음 |
|
어느 정도 일치 |
0.20 ~ 0.40 |
|
보통 일치 |
0.40 ~ 0.60 |
|
좋은 일치 |
0.60 ~ 0.80 |
|
매우 좋은 일치 |
0.80 ~ 1.00 |
■ F 척도 ( 445p)
정밀도와 재현율을 하나의 값으로 결합한 성능 척도를
F-척도(F-measure) 라고 한다
F-척도는 조화평균harmonic mean 을 이용해서 정밀도와 재현율을
결합한다.
2 x 정밀도 x 재현율 2 x TP
F척도 = ------------------------- = -------------------------
재현율 + 정밀도 2 x TP + FP + FN
문제266.
햄/스팸 메일을 분류하는 모델의 F 척도가 어떻게 되는가?

두 가지 방법으로 F 척도를 구해본다
2 x 정밀도 x 재현율 2 x TP
F척도 = ------------------------- = -------------------------
재현율 + 정밀도 2 x TP + FP + FN
2 * 0.9743 * 0.8306 = 1.6185
F 척도 =--------------------- = 1.6185/1.8049=0.8967
0.8306+0.9743=1.8049
2 * 152 = 304
F 척도 = ------------------------ = 304/339 = 0.8968
2*152 + 4 + 31 = 339
F-척도는 모델의 성능을 하나의 숫자로 설명하기 때문에
여러모델을 나란히 비교할 수 있는 편리한 방법을 제공한다.
하지만 F-척도는 정밀도와 재현율에 동일한 가중치를 할당하는 것으로
가정하는데, 이 가정이 항상 유효하지는 않다.
정밀도와 재현율에 다른 가중치를 사용해 F-점수를 계산하는 것도
가능하지만, 가중치를 선택하는 것이 최선의 경우에는 까다롭고
최악의 경우에는 임의적일 수 있다.
더 나은 방안은 F-점수와 같은 척도를 모델의 장단점을 좀 더 전역적으로
고려하는 방법과 결합해서 사용하는 것이다.
(+ 성능 트레이드오프 시각화)
■ 성능 트레이드 오프 시각화( 446p)
민감도와 특이도 또는 정밀도와 재현율과 같은 통계치가
모델의 성능을 하나의 숫자로 압축시키려고 한다면
시각화는 다양한 조건에서 학습자가 어떻게 실행 하는지 보여준다.
민감도, 특이도를 볼 수 있는 시각화 자료.
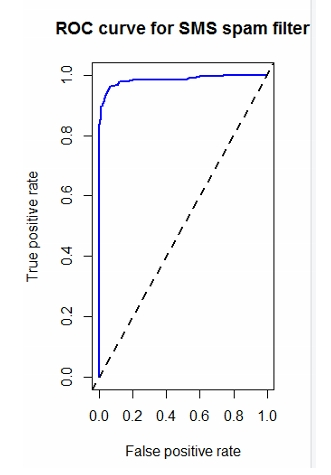
*ROC 곡선(447p)
Receiver Operating Characteristic curve
거짓긍정을 피하면서 참 긍정을 탐지하는 것 사이의 트레이드 오프를
관찰하는데 사용된다.

참 긍정률 (=민감도)
거짓 긍정률(= 1-특이도)
직선형 점선(="예측값이 없는 분류기")은 분류 못하는, 의미없는 모델.
각진형 점선(="완벽한 분류기")이 이상적인 모델.
위 둘 사이에 있는 실선형 곡선(="테스트 분류기")이 ROC 곡선이다.
ROC 곡선이 "완벽한 분류기"에 가까워질수록 분류기는 긍정 값을
더욱 잘 식별하게 된다.
이것은 AUC(Area Under the ROC Curve) 로 알려진 통계로 측정할 수 있다.
*AUC 란?
ROC 곡선이 쓸모없는 분류기를 나타내는 점선보다 완벽한 곡선에
가깝다는 것을 정량적으로 확인할 수 있는 수치
ROC 곡선의 아래 전체 영역을 측정한 값.
|
|
AUC 점수 |
|
A:뛰어남 |
0.9 ~ 1.0 |
|
B:매우우수/ 우수 |
0.8 ~ 0.9 |
|
C: 보통/양호 |
0.7 ~ 0.8 |
|
D: 불량 |
0.6 ~ 0.7 |
|
E: 판별되지않음 |
0.5 ~ 0.6 |
## Confusion matrixes in R ----
sms_results <- read.csv("sms_results.csv")
# the first several test cases
head(sms_results)
## Visualizing Performance Tradeoffs ----
library(ROCR)
pred <- prediction(predictions = sms_results$prob_spam,
labels = sms_results$actual_type)
# ROC curves
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf, main = "ROC curve for SMS spam filter", col = "blue", lwd = 2)
# add a reference line to the graph
abline(a = 0, b = 1, lwd = 2, lty = 2) #의미없는 선 표시하려고 넣은 코드
# calculate AUC
perf.auc <- performance(pred, measure = "auc")
str(perf.auc)
unlist(perf.auc@y.values)
[1] 0.9835862
■ 홀드아웃 방법 (p453)
holdout method
홀드아웃 방법이란 훈련 데이터셋과 테스트 데이터셋으로
분할하는 절차를 말한다.
이때 훈련 데이터를 2/3, 테스트 데이터를 1/3 으로 나눠서 훈련 시키는데
이때 훈련 데이터는 무작위로 샘플링하여 추출한다
그런데
무작위로 추출하 훈련 데이터중에서 대표적이지 않은 데이터가
추출되어 훈련될 가능성이 있다.(outlier이상치 가 섞임)
이런 가능성을 예방하기 위한 방법으로 반복 홀드 아웃(457p)이라는
기법이 있다.
# Holdout method
# using random IDs
random_ids <- order(runif(1000)) # setseed 대신 runif 사용
credit_train <- credit[random_ids[1:500],]
credit_validate <- credit[random_ids[501:750], ]
credit_test <- credit[random_ids[751:1000], ]
■ k -폴드 교차 검증 테스트
데이터 : credit.csv (부도예측)
모델 : C5.0 의사결정트리
"k-fold 교차검증을 통해서 credit 데이터로 부도예측을 하는
모델의 평균 카파지수를 확인하는게 목표가 된다"

데이터를 3개로 나눈다
훈련 train
검증 validation
테스트 test
검증과 테스트 데이터셋을 비교해서 최고의 kappa통계량을 뽑아낸다.
##C50을 이용한 최적의 kappa 통계량 구하기
# k-fold 교차검증
## Estimating Future Performance ----
# partitioning data
library(caret)
credit <- read.csv("credit.csv")
# using caret function
in_train <- createDataPartition(credit$default, p = 0.75, list = FALSE)
# caret 패키지의 층별 홀드아웃 샘플링 방식으로 파티션을 생성하는
# createDataPartition 함수를 사용한다.
credit_train <- credit[in_train, ]
credit_test <- credit[-in_train, ]
# 10-fold CV
folds <- createFolds(credit$default, k = 10)
str(folds)
credit01_test <- credit[folds$Fold01, ] # 01 번째를 test로
credit01_train <- credit[-folds$Fold01, ] # 01을 제외한 나머지를 train 으로
## Automating 10-fold CV for a C5.0 Decision Tree using lapply() ----
library(caret)
library(C50)
library(irr)
credit <- read.csv("credit.csv")
set.seed(123)
folds <- createFolds(credit$default, k = 10)
cv_results <- lapply(folds, function(x) {
credit_train <- credit[-x, ]
credit_test <- credit[x, ]
credit_model <- C5.0(default ~ ., data = credit_train)
credit_pred <- predict(credit_model, credit_test)
credit_actual <- credit_test$default
kappa <- kappa2(data.frame(credit_actual, credit_pred))$value
return(kappa)
})
str(cv_results)
mean(unlist(cv_results))
str(cv_results)
List of 10
$ Fold01: num 0.343
$ Fold02: num 0.255
$ Fold03: num 0.109
$ Fold04: num 0.107
$ Fold05: num 0.338
$ Fold06: num 0.474
$ Fold07: num 0.245
$ Fold08: num 0.0365
$ Fold09: num 0.425
$ Fold10: num 0.505
> mean(unlist(cv_results))
[1] 0.283796
■ 모델성능평가 요약
머신러닝분류모델의 성능을 평가하는 가장 일반적인 척도와 기술을
제시했다.
정확도는 모델이 얼마나 자주 정확한지를 관측하는 단순한 방법을
제공하지만, 드문 사건의 경우 실제 사건 비용이 사건의 발생 빈도에 반비례
하기 때문에 오해를 불러일으킬 수 있다.
혼돈행렬을 기반으로 하는 여러 척도들은 다양한 종류의 오류 비용 사이에
균형을 잘 포착한다.
민감도와 특이도, 정밀도와 재현율 사이에 트레이드오프를 면밀히
검토하면 현실 세계에서의 오류의 의미에 대해 생각할 수 있는
유용한 도구가 될 것이다.
ROC 곡선과 같은 시각화는 이 목적에 많은 도움이 된다.
■ 모델 성능평가 척도 총 정리
|
1 |
정확도 |
|
2 |
정확도 외에 다른 성능척도를 출력하기 위한 기본 데이터 수집 |
|
3 |
카파 통계량 |
|
4 |
민감도 |
|
5 |
특이도 |
|
6 |
정밀도 |
|
7 |
재현율 |
|
8 |
F 척도 |
|
9 |
ROC 척도 |
|
10 |
AUC 수치 |
사용할 데이터-> 독일 은행의 채무 불이행자를 예측을 위한 데이터
(credit.csv)
■ 독일 은행의 대출 여부 데이터로 의사결정 트리 실습
#1. 데이터를 로드한다.
setwd("d://data")
credit <- read.csv("credit.csv")
set.seed(31)
credit_shuffle <- credit[sample(nrow(credit)), ]
#2. 데이터를 9 대 1로 나눈다
train_num<-round(0.9*nrow(credit_shuffle),0)
credit_train <- credit_shuffle[1:train_num,]
credit_test <- credit_shuffle[(train_num+1):nrow(credit_shuffle),]
#3. C5.0 패키지와 훈련데이터를 이용해서 모델을 생성한다.
library(C50)
credit_model <- C5.0(credit_train[, -17], credit_train[,17] )
# 17번째가 default
#4. 모델과 테스트 데이터로 결과를 예측한다.
credit_result <- predict( credit_model, credit_test[ , -17] )
credit_result
credit_test[ , 17]
#5. 이원 교차표로 결과를 살펴본다.
library(gmodels)
CrossTable( credit_test[ , 17] , credit_result )
| credit_result
credit_test[, 17] | no | yes | Row Total |
------------------|-----------|-----------|-----------|
no | 64 | 11 | 75 |
| 0.267 | 1.067 | |
| 0.853 | 0.147 | 0.750 |
| 0.800 | 0.550 | |
| 0.640 | 0.110 | |
------------------|-----------|-----------|-----------|
yes | 16 | 9 | 25 |
| 0.800 | 3.200 | |
| 0.640 | 0.360 | 0.250 |
| 0.200 | 0.450 | |
| 0.160 | 0.090 | |
------------------|-----------|-----------|-----------|
Column Total | 80 | 20 | 100 |
| 0.800 | 0.200 | |
------------------|-----------|-----------|-----------|
x<-CrossTable(credit_test[,17], credit_result)
x$t
y
x no yes
no 64 11
yes 16 9
정확도 : TRUE 값 / 전체
sum(x$t) # 전체갯수
(x$t[1]+x$t[4])/sum(x$t)
0.73
#6. credit_results.csv 를 생성한다.
# obtain the predicted probabilities
credit_test_result <- predict( credit_model, credit_test[ , -17] )
credit_test_result # 예측라벨
credit_test_prob <- predict(credit_model, credit_test[ , -17], type = "prob") # prob=확률
head(credit_test_prob)
# 확률을 보여주는데
# 기준은 cut-off 로 정해준다. 예를 들어 cut-off 0.6면 0.6보다 큰 값만 no(채무이행자)로 포함시킨다.
# combine the results into a data frame
credit_results <- data.frame(actual_type = credit_test[ , 17],
predict_type = credit_test_result,
prob_yes = round(credit_test_prob[ , 2], 5), # yes가 2번째 열
prob_no = round(credit_test_prob[ , 1], 5))
head(credit_results)
# uncomment this line to output the sms_results to CSV
write.csv(credit_results, "credit_results.csv", row.names = FALSE)
▣ 2. 정확도 확인하는 코드
"학습자가 맞거나 틀린 경우의 비율"
x <- CrossTable( credit_test[ , 17] , credit_result )
x$t
sum(x$t)
x$t[1,1] + x$t[2,2]
x$t[1,1] + x$t[2,2]/sum(x$t)
▣ 3. 카파 통계량 (p 440)
"두 관찰자간의 측정 범주값에 대한 일치도"
install.packages("irr")
kappa2( credit_results[1:2])
Cohen's Kappa for 2 Raters (Weights: unweighted)
Subjects = 100
Raters = 2
Kappa = 0.229
z = 2.31
p-value = 0.0209
▣ 4. 민감도 (p 442)
"실제 참인것 중에서 참이라고 예측한 비율"
install.packages("ipred")
library(ipred)
library(caret)
sensitivity(credit_results$predict_type, credit_results$actual_type, positive="yes")
0.36
▣ 5. 특이도 (p 442)
"실제 거짓인것중에서 거짓으로 예측한 비율 "
library(caret)
specificity(credit_results$predict_type, credit_results$actual_type, nagative="no")
0.36
▣ 6. 정밀도 (p 444)
"스펨 메세지로 예측한것들 중에 실제로 스펨의 비율"
"정밀도 = (예측타겟=실제타겟) / 타겟 "
library(caret)
posPredValue(credit_results$predict_type, credit_results$actual_type, positive="yes")
0.45
▣ 7. 재현율
"실제 스펨 메세지 중에서 스펨 메세지로 예측한 비율 (민감도와 같다)"
library(caret)
sensitivity(credit_results$predict_type, credit_results$actual_type, positive="yes")
0.36
▣ 8. F척도 (p445)
"정밀도와 재현율을 하나의 값으로 결합한 성능척도"
참조내용 :
2 x 정밀도 x 재현율 2 x 0.9743 x 0.8306
F척도 = ------------------------ = ---------------------
재현율 + 정밀도 0.8306 + 0.9743
f<-(2*pv*sen)/(pv+sen)
# pv <- posPredValue , sen <- sensitivity
f <- (2*0.9743 * 0.8306) / (0.8306 * 0.9743)
f
0.4
▣ 9. Roc 커브
"거짓긍정을 피하면서 참 긍정을 탐지하는것"
참조코드
## Confusion matrixes in R ----
credit_results <- read.csv("credit_results.csv")
# the first several test cases
head(credit_results)
## Visualizing Performance Tradeoffs ----
library(ROCR)
pred <- prediction(predictions = credit_results$prob_yes,
labels = credit_results$actual_type)
# predictions 에 확률 집어넣어야함
# ROC curves
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf, main = "ROC curve for SMS spam filter", col = "blue", lwd = 2)
# add a reference line to the graph
abline(a = 0, b = 1, lwd = 2, lty = 2)
# calculate AUC
perf.auc <- performance(pred, measure = "auc")
str(perf.auc)
unlist(perf.auc@y.values)
▣ 10. AUC 수치
"roc 곡선이 쓸모없는 분류기를 나타내는 점선보다 완벽한 곡선에
가깝다는것을 정량적으로 확인할 수 있는 수치 "

문제276.
독버섯을 분류하는 모델의 아래의 성능척도를 출력하시오
#======================================================================
mushroom<-read.csv("mushrooms.csv",stringsAsFactors = TRUE)
#1. 데이터를 로드한다.
head(mushroom)
names(mushroom)
nrow(mushroom) # 8124
set.seed(11)
mushroom_shuffle <- mushroom[sample(nrow(mushroom)), ]
#2. 데이터를 9 대 1로 나눈다
train_num<-round(0.9*nrow(mushroom_shuffle),0)
mushroom_train <- mushroom_shuffle[1:train_num,]
mushroom_test <- mushroom_shuffle[(train_num+1):nrow(mushroom_shuffle),]
#3. mushroom 은 JRipper 가 가장 정확도가 높았다.
# JRip 모델을 이용해서 훈련데이터 모델을 만든다
library(RWeka)
mushroom_model <- JRip(type~. , data=mushroom_train)
# 17번째가 default
#4. 모델과 테스트 데이터로 결과를 예측한다.
mushroom_result <- predict(mushroom_model, mushroom_test[ , -1] )
head(mushroom_result)
#5. 이원 교차표로 결과를 살펴본다.
library(gmodels)
CrossTable( mushroom_test[ , 1] , mushroom_result )
x<-CrossTable(mushroom_test[,1], mushroom_result)
x$t
sum(x$t) # 전체갯수
(x$t[1]+x$t[4])/sum(x$t) # 정확도
#6. credit_results.csv 를 생성한다.
# obtain the predicted probabilities
mushroom_test_result <- predict(mushroom_model, mushroom_test[ , -1] )
head(mushroom_test_result) # 예측라벨
mushroom_test_prob <- predict(mushroom_model, mushroom_test[ , -1], type = "prob") # prob=확률
head(mushroom_test_prob)
# 확률을 보여주는데
# 기준은 cut-off 로 정해준다. 예를 들어 cut-off 0.6면 0.6보다 큰 값만 no(채무이행자)로 포함시킨다.
# combine the results into a data frame
mushroom_results <- data.frame(actual_type = mushroom_test[ , 1],
predict_type = mushroom_test_result,
prob_yes = round(mushroom_test_prob[ , 2], 5), # yes가 2번째 열
prob_no = round(mushroom_test_prob[ , 1], 5))
head(mushroom_results) # poisonous 가 yes
# uncomment this line to output the sms_results to CSV
write.csv(mushroom_results, "mushroom_results.csv", row.names = FALSE)
#install.packages("irr")
#library(irr)
kappa2( mushroom_results[1:2]) # 확률 뺀 actual, predict 만 가져와서 카파통계 돌림
#install.packages("ipred")
library(ipred)
library(caret)
# 민감도
sensitivity(mushroom_results$predict_type, mushroom_results$actual_type, positive="poisonous")
# 특이도
spe<-specificity(mushroom_results$predict_type, mushroom_results$actual_type, nagative="edible")
# 정밀도
pv<-posPredValue(mushroom_results$predict_type, mushroom_results$actual_type, positive="poisonous")
# 재현율
sen<-sensitivity(mushroom_results$predict_type, mushroom_results$actual_type, positive="poisonous")
f<-(2*pv*sen)/(pv+sen)
f
## Confusion matrixes in R ----
mushroom_results <- read.csv("mushroom_results.csv")
# the first several test cases
head(mushroom_results)
## Visualizing Performance Tradeoffs ----
library(ROCR)
pred <- prediction(predictions = mushroom_results$prob_yes,
labels = mushroom_results$actual_type)
# ROC curves
perf <- performance(pred, measure = "tpr", x.measure = "fpr")
plot(perf, main = "ROC curve for SMS spam filter", col = "blue", lwd = 2)
# add a reference line to the graph
abline(a = 0, b = 1, lwd = 2, lty = 2)
# calculate AUC
perf.auc <- performance(pred, measure = "auc")
str(perf.auc)
unlist(perf.auc@y.values)

■ mushroom.csv 의 모델 성능평가 척도 총 정리
|
정확도 |
100 |
|
카파통계량 |
1 |
|
민감도 |
1 |
|
특이도 |
1 |
|
정밀도 |
1 |
|
재현율 |
1 |
|
F 척도 |
1 |
|
ROC 척도 |
직각 |
|
AUC 수치 |
1 |
AUC 값의 범위는 0~1입니다.
ROC를 수치화 시킨 것.
예측이 100% 잘못된 모델의 AUC는 0.0이고
예측이 100% 정확한 모델의 AUC는 1.0입니다.
AUC = AUROC (the Area Under a ROC Curve) : ROC 커브의 밑면적을 구한 값이 바로 AUC. 이 값이 1에 가까울수록 성능이 좋다.
AUC 해석 : 1로 예측하는 기준을 쉽게 잡으면 민감도는 높아진다. 그대신 모든 경우를 1이라고 하므로 따라서 특이도가 낮아진다. 그러므로 이 두 값이 둘다 1에 가까워야 의미가 있다. 그래서 ROC커브를 그릴때 특이도를 1-특이도를 X축에 놓고, Y축에 민감도를 놓는다. 그러면 x=0일때 y가 1이면 가장 최고의 성능이고, 점점 우측 아래로 갈수록, 즉 특이도가 감소하는 속도에비해 얼마나 빠르게 민감도가 증가하는지를 나타냄.
만약 AUC = 0.5라면, 특이도가 감소하는 딱 그만큼 민감도가 증가하는 것으로, 즉 어떤 기준으로 잡아도 민감도와 특이도를 동시에 높일 수 있는 지점이 없다는 것이다.
AUC가 0.5라면, 특이도가 1일때 민감도는 0, 특이도가 0일때 민감도는 1이되는 비율이 정확하게 trade off관계로, 두값의 합이 항상 1이다.
그러므로 AUC값은 전체적인 민감도와 특이도의 상관 관계를 보여줄 수 있어 매우 편리한 성능 척도에 기준이다.


